- ライター:工藤 聖乃
- 2020年ネットワンシステムズに新卒入社。
新製品の技術検証、新技術を組みあわせた新しいソリューション開発や検証業務に従事。
2022年からは現在のデジタルマーケティング基盤チームに参画
目次
昨今、COVID-19の影響により、さまざまな場面で感染症を避けるために「3密(密閉、密集、密接)」を控えることを求められています。オフィスへの出社が制限され、会議室を利用するにあたっても人数制限を設け社員が「3密」な状況で働くことのないようルールが必要です。
弊社では、会議室におけるCO₂量を測定し、あらかじめ設定されたCO₂量を超えると3段階でアラート(ランプが点灯、ビデオ会議端末にポップアップ)を出すという検証をおこなっております。今回はその検証の一部として、設定されたCO₂量が適切であるかデータ分析にチャレンジしました。
前編では分析に至った背景やデータ収集の詳細や構成、進め方、データの前処理についてご紹介いたしました。
後編となる本ブログでは、分析手法、結果からの考察についてご紹介いたします。
また、データ分析初学者として所感を綴らせていただきました。
検証環境
| 使用したデータの期間 | 2019年1月1日~2019年12月31日(休日を含む) |
| テストデータ | 2020年1月1日~2020年4月26日(休日を含まない、1人以上使用している場合) |
| 時間 | 9:00~10:00 |
| 場所 | 本社(JPタワー)にある会議室一室(最大収容人数 8人、約30㎥) |
| データ分析に使用したツール | Outlookの会議予約状況、CO₂センサー(SEIKO社製)、Elastic Stack、Excel、人感センサー(SEIKO社製)、(RapidMiner) |
データ収集の詳細や構成、進め方、データの前処理につきましては、前編にてご紹介しております。
結果と考察
線形回帰で分析をおこないました。線形回帰を用いた理由として、比較的単純で初学者として理解しやすいことが挙げられます。Excelで使用した式、関数は以下の通りです。
|
◇増加値=SLOPE(x:予測データ人数、y:開始時PPM-終了時PPM)×人数+INTERCEPT(x:予測データ人数、y:開始時PPM-終了時PPM) ◇RMS(SQRT(二乗和/データ数))=二乗和(SUMSQ(実際値-予測値))/データ数(COUNT) (◇予測人数=(実際値-INTERCEPT(x:予測データ人数、y:開始時PPM-終了時PPM)SLOPE(x:予測データ人数、y:開始時PPM-終了時PPM)
※線形回帰…ある変数の値を、他の変数の値から基づき予測 ※予測値…線形回帰における予測値 ※RMS…値を二乗し、二乗の平均を算出し、その平方根をとったもの。 N個のデータ、各データの x の値を (i = 1, 2, ..., N)とするとRMS(x)は この値の大きさにばらつき具合も比例する 例:A氏とB氏がテストを受験どちらも50点の場合 →平均 50点・RMS 50 A氏が100点、B氏が0点の場合 →平均 50点・RMS 70.7 |
前処理を施したデータをこれらの式にあてはめ各人数における予測値を算出すると、RMS値が69.332となり誤差が大きく、予想が外れているのではないかと読み取れてしまいます。そこで、この数値が妥当か否かを分析していきました。
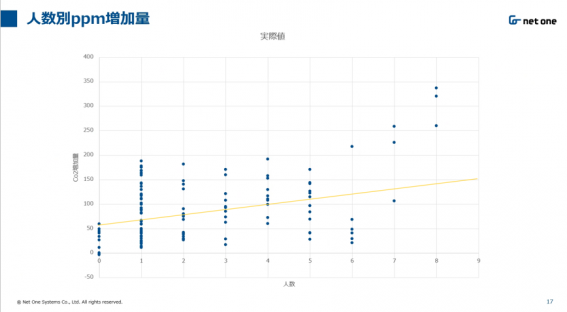
図1 人数別ppm増加量(終了時ppm-開始時ppm)、黄色の線は増加量の予測値を表す
RMS値が高く予測が外れているかの確認をおこなうために、それぞれの人数ごとにおける予測値との差を確認いたしました。図1は前処理をおこないppm増加量を人数別にまとめたグラフです。このグラフからもわかるように1人、2人、3人の場合、ばらつきが多く見受けられました。
そこで次にデータをヒストグラムで図解し同じ人数の場合でどれだけのばらつきが生じているかの確認をおこないました。
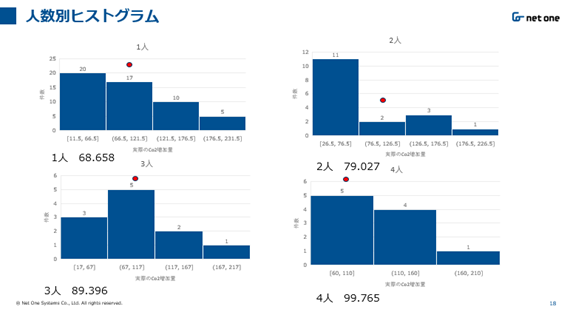
図2 終了時ppm―開始時ppmのヒストグラムと赤い丸は予測値を表す
図2のヒストグラムから2人の場合を除き1人、3人、4人の場合予測値の付近に分布が集中していることが図から読み取れ、おおむね予測値と実際の値に差がないように伺えます。しかし、0人の場合、予測値58.289(表1)に限らず、実際の値も予測値に近い50付近に収束しており、人が会議室に存在していないにもかかわらずCO₂が増加していることに疑問を感じました。
そこで、予測値58.289が数値として正しいのかデータを見直し、何が要因であるか確認をおこないました。
しかし、確認をおこなう途中、0人の場合のデータ数が少ないという事態に陥ってしまったため、データ数を増やすために土日データを追加し、再度考察をおこないました。
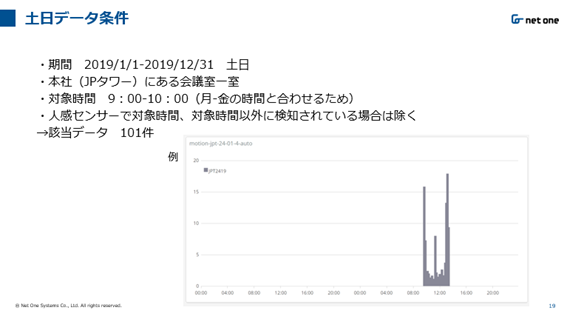
図3 土日データの条件と人感センサーによる確認
土日のデータは図3を条件に収集をおこないました。図3にあるように、Outlook上で誰も使用していないにもかかわらず、CO₂量が高い日が何日か見受けられ、そのような場合には人感センサーの数値の確認をおこない、検知されている場合、それらのデータを除きました。
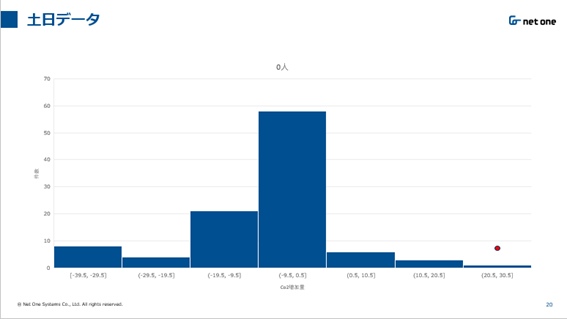
図4 終了時ppm―開始時ppmのヒストグラムと赤い丸は予測値を表す
土日データをもとに人がいない場合をまとめました。しかし、図4にあるように分布は0から-10に近い値に収束しました。
これらのことから平日には50に近い値が出ていることから会議室の周りの人や外気それらに要因があると考えられるのではないかと考えます。
以上の分析より、今回のデータから線形回帰をおこない生成された予測値は、ネットワンの会議室における実際の数値に近い値が予測されていることが分かりました。これらの数値をもとにアラートのCO₂量を設定することでより精度の高いアラートを出すことが可能であると考えられます。
しかし、土日データのように外的要因も考えられることから、今後は外気データなどを増やし、深堀が必要です。
おわりに
データ分析を初めて経験し、実際におこなってみると、その大変さを身に染みて実感しました。
一番苦労した作業は前編で綴られている、前処理で思うように予測値と実際の値が合わず、外れ値を選定する作業です。外れ値を選定するのに時間がかかった要因として、表示されているデータをそのまま読み取ってしまい、そのデータから何が言えるかにこだわってしまいました。初学者である私は、すぐにデータに目を向けてしまいがちになっていましたが、「目的を明確にし、それを検証・分析するためにデータや方法を考える」この繰り返しがデータ分析をする上で大切であるということを今回のデータ分析を通じて学ぶことができました。
※本記事の内容は執筆者個人の見解であり、所属する組織の見解を代表するものではありません。